The Earth-bending Scale of the Great Lakes

The Earth-bending Scale of the Great Lakes

On a gloomy afternoon last week, some friends of mine and I drove from Lafayette, IN to the Indiana Dunes State Park. It was a bit too cold and dry to be outdoors for my taste. But I was visiting Indiana only for a few days, and I really wanted to visit Lake Michigan, so I decided that it would be worth it.

As we hiked up along the sandy dunes of the State Park’s Trail 8, we began to get a good view of Lake Michigan. This was my second time visiting the lake, and I was hoping to see the sparkling blue waters of the lake under a clear sky. Instead, the water reflected the dull gray color of the overcast sky.

As I realized a little later, the cold and dry weather was not all bad, as thanks to it, we got to witness a very interesting phenomenon. As we reached the highest point along Trail 8, roughly 150 ft above the water of Lake Michigan, we got to see the Chicago skyline in the distance. Coupled with my shortness of breath from all the dune climbing, it gave me the feels of being an ancient nomad, wandering the forests and accidentally stumbling upon the sight of a great civilization in the distance. (cue inspiring music in the background)

It was a terrific sight to behold, and I instantly regretted not bringing my DSLR along. The wide field of view of my smartphone camera meant that the skyline — far in the distance — would look smaller in the picture than it appeared in real life, but here’s something to give you an idea (and trust me, it looked much better in real life):

Why does it appear smaller?

We decided to venture down to the waters of the lake, and on our way down, I noticed that the skyline had started to appear smaller. It had started to look as though part of the skyline had submerged…it was a strange sight to see at first. After all, when there’s a city across the lake and you can see it, why would its skyline appear partially submerged in the lake’s water when you’re at the same altitude as the lake?

Take a look at the pictures below — both pictures were taken with my Pixel 3, with no zoom in either case (although I cropped the pictures later to roughly equal proportions). Forgive me for not carrying my DSLR on that day, and for subjecting you to cropped and contrast-enhanced pictures taken on a smartphone, but they show the effect clearly enough.

I figured that it’s safe to assume that there’s no catastrophic tsunami-type flooding of Chicago happening — at least, the weather forecast hadn’t predicted any such thing! (Although in my experience you can never trust weather forecasts in North America.) Jokes apart, I quickly realized that the skyline had appeared smaller at ground level because of — wait for it — the earth’s curvature.

The earth ain’t flat

As strange as it sounds to be able to observe the effect of our planet’s non-flatness while on the ground (as opposed to floating around inside the International Space Station), it turns out that you can — with some help. Note that it is the effect of the earth’s curvature that one can observe from ground level, and not the curvature itself; for that, you’d need to be at a much higher altitude!

Take a look at the sketch below: it’s rough, and it’s not to scale, but it paints a picture of the geometry of the problem. Imagine that you’re at ground level, standing in front of your favorite tower (preferably a tall one). If you were to walk backwards away from the tower on perfectly flat ground while still facing it, for the first miles or two, the tower would appear smaller, but you would be able to see it in its entirety: from bottom to top. As you walk farther away (say, a few to 10s of miles), however, the earth’s curvature begins to play a role in how much of it you can see.

At far enough distances, the earth curves enough for you to not be able to see the bottom of the tower anymore! This would happen even if the land everywhere were perfectly (locally) flat, i.e. in the absence of any hills and valleys. I won’t go through the gory details of the trigonometry here, but [here’s a fun calculator](http://dizzib.github.io/earth/curve-calc/index.html?d0=30&h0=10&unit=imperial) made by Github user ‘dizzib’ that you can play with. Here’s another one if you’d like to cross verify the results that you see.

Crunching the numbers

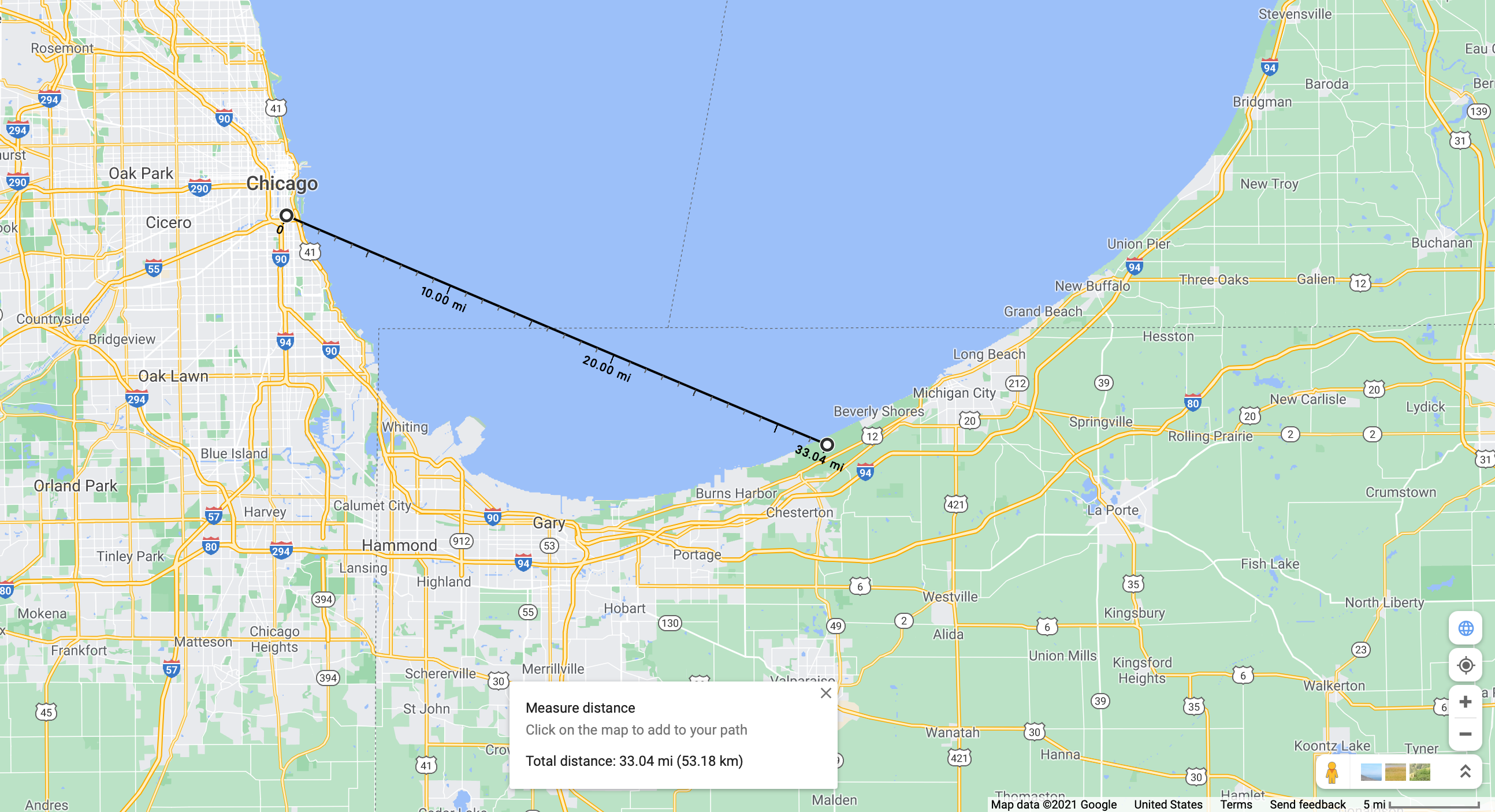
If you measure the point-to-point distance between Chicago downtown to Indiana Dunes State Park on Google Maps, it comes out to be about 33 mi. The height of the Willis Tower — the tallest tower in Chicago — is about 1450 ft. For a 6 ft tall person standing at the ground level, you can use this calculator to estimate that the minimum height of a tower/structure for you to be able to see it is 600 ft. In other words, anything shorter than 600 ft would not be visible in the skyline view.

For the same distance, if the same person were to stand on top of a hill that’s about 150 ft tall (approximately the elevation above Lake Michigan of the highest point of Trail 8), the calculator will show you that the minimum structure height for visibility 33 mi away is now only 216 ft.

The difference in heights for visibility is about 380 ft, which is approximately 25% of the height of the Willis Tower! That difference in apparent height can also be resolved by the human eye: with an angular resolution of 1 arcminute, the human eye is capable of resolving features larger than approximately 50 ft for objects and features that are 33 mi away. Given that the difference in visible skyline levels is over 200 ft, it makes sense that one is able to observe the effect of earth’s curvature!

A caveat

All of the geometrical calculations above make sense under the assumption that light travels in straight lines. This is true on most days, but on warmer days when the air temperature is higher close to ground level, light can bend because of atmospheric temperature-gradient-induced refraction. Although I wasn’t a fan of the sub-zero weather that afternoon last week, it did mean that the effects of atmospheric refraction were minimal. (Side note: temperature-gradient-induced atmospheric refraction is also why you see mirages of oases in deserts!)

On warmer days, therefore, the math above is no longer accurate, as light no longer travel in the straight lines that we drew for simple calculation. In fact, it turns out that you would be able to see the Chicago skyline even farther away than the calculators above would predict! A simplified illustration of how this could be, in the presence of bending due to refraction, is shown in the sketch below.

See this article published by ABC News, where they discuss the spotting of a mirage of the Chicago skyline **above Lake Michigan — not in nearby Indiana but rather all the way in Michigan over **50 miles away from Chicago! If you were to use any of the calculators I linked above, you would see that from a 50 mi distance, you wouldn’t be able to see even the Willis Tower, standing at ground level. The presence of warmer air, however, makes it possible for one to “see beyond the horizon”, in a sense.

‘Great’ Lakes indeed

To me, observing this phenomenon live was not only a cool demonstration of the non-flatness of earth, but also a humbling display of the scale of the Great Lakes. A straight line drawn from Indiana Dunes State Park to Chicago barely covers a small fraction of Lake Michigan, but that line would still be long enough for us to be able to see the effects of the earth’s curvature.

I typically associate going to a nearby lake or water body with serenity, a sense of calm, and fresh air. The Great Lakes do all of that, but they also leave you humbled. They leave you with a fascination for not just the lakes, but also for the size, scale and diverse topography of our planet.

Unlike the oceans of our world, the Great Lakes demonstrate to us our puny size, and perhaps our eventual irrelevance, in a way that is intimidating yet not overwhelming, and in a way that is relatable yet too ‘great’.

This story was originally published by the author on Medium.